Bei der statistischen Auswertung ist nicht nur die Mitte interessant, sondern auch die Extreme. Um beim klassischen Beispiel der Feedbackbogenauswertung zu bleiben, also wie stark sich die Einschätzungen der Teilnehmer unterscheiden, was die beste und was die schlechteste Bewertung war. Zur Beschreibung dessen eignen sich mehrere Maße:
Als Maß für die Streuung wird in den meisten Auswertungen standardmäßig neben dem arithmetischen Mittel die Standardabweichung angegeben. Je größer die Standardabweichung, umso stärker unterscheiden sich die Werte vom arithmetischen Mittel, sie streuen. Manchmal wird statt der Standardabweichung auch die Varianz einer Verteilung angegeben. Dabei handelt es sich allerdings lediglich um die quadrierte Standardabweichung und somit nicht um ein grundlegend anderes Streuungsmaß.
Mit Angabe der Standardabweichung oder der Varianz verbessert sich die die Beschreibung und Vergleichbarkeit unterschiedlicher Verteilungen. So ist schnell ersichtlich, ob die Teilnehmer des diesjährigen Seminars eine einheitlichere Bewertung abgegeben haben, als die des letzten Jahres. Jedoch kann bei gleichem arithmetischen Mittel und gleicher Standardabweichung die Verteilung sehr unterschiedlich aussehen. Die beiden Werte sagen noch nichts darüber aus, ob die Werte gleich verteilt sind, ob mehr Werte oberhalb oder mehr Werte unterhalb des Mittels liegen. Die folgenden beiden Darstellungen hypothetischer Seminarbewertungen machen dies deutlich.
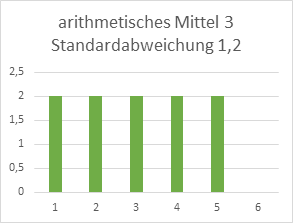
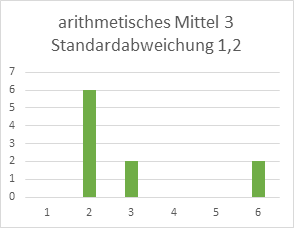
Außerdem ist unklar, ob alle Werte etwa gleich weit von der Mitte entfernt liegen oder viele sehr nah dran und nur einige wenige sehr weit weg. Solche außergewöhnlich hohen oder niedrigen Werte werden als „Ausreißer“ bezeichnet. Im zweiten oben angegebenen Beispiel etwa könnte man die beiden Bewertungen mit 6 Ausreißer als Ausreißer bezeichnen. Um Ausreißer abzubilden, kann der Beschreibung eine Angabe zum kleinsten und größten vorkommenden Wert, also zum Minimum und Maximum, hinzugefügt werden.
Ausreißer – also einzelne extrem Werte – sind umso bedeutender, je weniger Werte insgesamt betrachtet werden. Das heißt, wenn nur wenige Mitarbeiter an einer Befragung teilnehmen, können die beschreibenden Maße wie arithmetisches Mittel und Standardabweichung umso stärker von einzelnen beeinflusst werden. Angenommen im obigen Beispiel hatte der Referent einfach Pech und zwei notorisch uninteressierte Teilnehmer im Kurs, die diesen mit 6 bewertet haben. Während sie in diesem Fall mit zehn Teilnehmern den Durchschnitt von 2,25 auf 3 senken, würden sie denselben Durchschnitt im Fall von 100 Teilnehmern lediglich auf 2,33 senken. Bei 1000 befragten Teilnehmern fallen zwei Ausreißer dann kaum mehr ins Gewicht.
Statistische Maße sind hilfreich. Sinnvoll sind diese jedoch insbesondere ab einer Zahl von etwa 100 Befragten. Gerade im Businesskontext, ob bei Befragungen auf Abteilungsebene oder im Rahmen von 360-Grad Feedback, werden dennoch häufig statistische Auswertungen auf Grundlage der Bewertungen weniger gemacht. Für diese Fälle eignen sich Darstellungen der gesamten Verteilung, wie oben zur Verdeutlichung genutzt, wesentlich besser.
Zum Nachlesen:
- Wer mehr zur Berechnung der Standardabweichung nachlesen möchte, wird im Statistik-Lexikon von statista fündig.
- Eine Kurzanleitung zur Berechnung in Excel finden Sie hier.