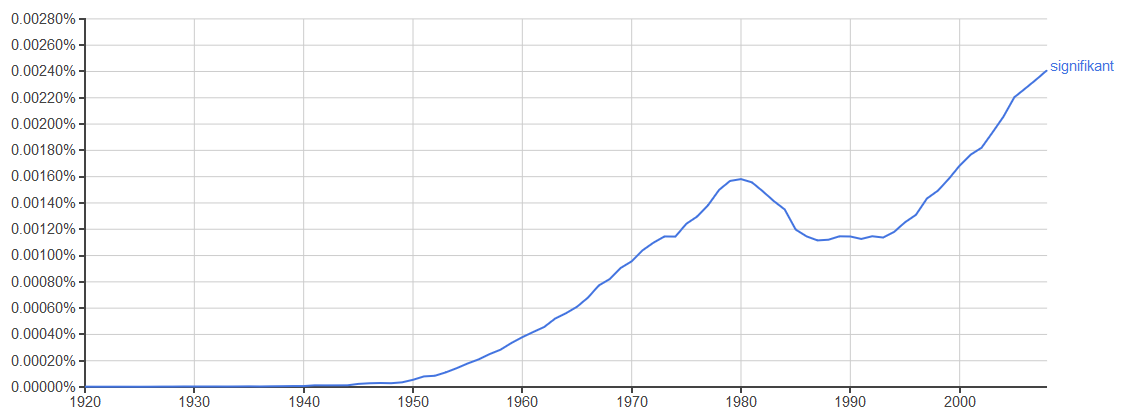
Das Wörtchen ’signifikant‘ hat Konjunktur. Die Berliner Morgenpost etwa nannte Jogi Löws Veränderung der Abwehrkette für das Viertelfinale der Fußball-EM ’16 signifikant und bei Cicero kann man aktuell lesen, dass sich unter den Anhängern des Brexits „signifikant häufiger Personen mit niedrigem Bildungsniveau und geringem Sozialstatus“ finden. Der gefühlt inflationäre Gebrauch des Wortes ist keine Illusion. Die Häufigkeit mit der signifikant verwendet wird, nimmt seit Mitte der 90er Jahre kontinuierlich zu. Doch was bedeutet signifikant eigentlich?
Der Duden nennt drei Wortbedeutungen: Im allgemeinen Sprachgebrauch bedeutet signifikant vereinfacht entweder deutlich oder charakteristisch. Die dritte Bedeutung bezieht sich auf die Statistik. Der statistische Begriff steht für einen Zusammenhang, der zu groß ist um noch als zufällig zu gelten. Hier geht es also ebenfalls um einen deutlichen Zusammenhang. Allerdings erfordert das Urteil ’statistisch signifikant‘ eine genaue Berechnung und geht damit über das subjektive Urteil ob ein Unterschied deutlich erkennbar ist, hinaus.
Signifikanz als rhetorisches Mittel für Glaubwürdigkeit
Im Kontext einer wissenschaftlichen Studie kann sich der Leser sicher sein, dass das Wort signifikant im statistischen Sinne verwendet wird. Im Fall der deutschen Fußballabwehr ist die Wortbedeutung hingegen klar nicht statistisch. Schwieriger wird es in Texten wie dem über die Brexit-Befürworter – einem nicht-wissenschaftlichen Text, der dennoch Zahlen und Statistiken nennt. Hier ist plötzlich nicht mehr klar, von welcher Bedeutung von signifikant hier die Rede ist. Die meisten Menschen nehmen alles was mit Zahlen untermauert wird ernster – unter Umständen sogar unabhängig davon, was für Zahlen präsentiert werden. Diese Zahlengläubigkeit überträgt sich vermutlich auch auf alles was mit dem Begriff signifikant geadelt wird.
Was heißt statistisch signifikanter Zusammenhang?
Beim statistischen Signifikanz-Begriff geht es darum, dass ein gemessener Zusammenhang mit einer bestimmten Wahrscheinlichkeit nicht zufällig ist, also zutrifft. Er kommt immer dann zur Anwendung, wenn Anhand einer Stichprobe die Gesamtheit geschlossen werden soll. So basieren die Zahlen zu den aktuellen Analysen über das Wahlverhalten der Briten in der Brexit-Abstimmung lediglich auf einer Befragung eines Teils der Wähler. Daraus versucht man nun Rückschlüsse auf die gesamte Bevölkerung zu ziehen. In einem ersten Schritt wird lediglich festgestellt, ob sich unter den befragten Brexit-Befürwortern mehr Menschen mit geringem Bildungsniveau befinden als unter den befragten Brexit-Gegnern. Erst durch Berechnungen lässt sich jedoch feststellen, wie hoch die Wahrscheinlichkeit ist, dass dies lediglich durch eine zufällige Auswahl zustande gekommen ist und nicht auf die Gesamtheit der britischen Wähler zutrifft. Ist die Wahrscheinlichkeit für einen solchen Fehlschluss geringer als fünf Prozent spricht man davon, dass der Bildungsunterschied zwischen Brexit-Befürwortern und -Gegnern signifikant auf dem Fünf-Prozent-Niveau ist. Der statistische Begriff ist also zunächst ebenfalls relativ. Soweit nicht anders angegeben, bezieht sich die statistische Signifikanz jedoch meist auf genau diese Fünf-Prozent-Schwelle.
Signifikant gleich starker Zusammenhang?
Statistische Signifikanz sollte nicht mit der Stärke eines Zusammenhangs verwechselt werden. Im obigen Beispiel bezieht sich die Stärke des Zusammenhangs darauf, wie viel höher der Anteil von Menschen mit niedrigem Bildungsniveau in der Gruppe der Brexit-Befürworter liegt als in der Gruppe der Brexit-Gegner. Ob ein Zusammenhang signifikant ist oder nicht, sagt hingegen etwas darüber aus, wie sicher man sich darüber sein kann, dass sich das Ergebnis der Stichprobe auf die Gesamtbevölkerung übertragen lässt. Signifikanz sagt also lediglich, ob man überhaupt von einem Zusammenhang ausgehen kann. Wären alle Briten befragt worden, ließe sich die Höhe des Zusammenhangs sicher feststellen. Das Konzept der Signifikanz ist in dem Fall obsolet.
Ein Fehlschluss auf 20 Fälle
Selbst wenn aus dem Kontext klar wird, dass es sich um einen statistisch signifikanten Zusammenhang handelt, ist noch Vorsicht geboten. Ob ein Unterschied auf einem gegebenen Niveau signifikant ist, hängt nicht nur vom Unterschied ab, sondern auch von der Anzahl der Beobachtungen:
Im Fall der negativen Auswirkungen des Pendelns zum Beispiel geht es um Unterschiede von 0.02 auf einer Skala von 1-5. Bei mehr als 10.000 Fällen sind diese Unterschiede signifikant. Ihre Bedeutung ist jedoch unabhängig von der statistischen Signifikanz zu beurteilen. Bei Verwendung des gängigen Signifikanzniveaus ist die gezogene Schlussfolgerung außerdem immerhin noch im Durchschnitt in einem von 20 Fällen falsch. Auch vor dem Hintergrund immer besserer und größerer Datensätze setzt sich in der Wissenschaft mehr und mehr das Ein-Prozent-Signifikanzniveau durch. Also nur noch ein Fehlschluss auf 100 Fälle.
Zum Nachlesen:
- Eine ausführliche Erklärung zum statistischen Signifikanz-Begriff mit Links zu weiteren relevanten Begriffen und Konzepten bietet das Statistik-Lexikon von statista.